数学历史|阿波罗尼斯圆到底是个什么圆?
数学历史|阿波罗尼斯圆到底是个什么圆?
今天课上讲解模考试题,其中一道填空题的题干提到了“阿波罗尼斯圆”。有的学生对“阿波罗尼斯圆”这个名词有点懵,觉得这题会有难度。
又是被陌生题干吓怕了的学生。
学生们你一言我一语的在课堂上和我对话大致如下。
我就问“阿波罗尼斯家的圆,圆不圆?”
A学生答“圆,妥妥的圆!”
我说“是圆就按圆的做法做啊!”
B学生说“但是我觉得阿波罗尼斯圆可能是国外的圆,然后,那个,然后。。”
我说“然后啥啊?这题干应该是希腊文的呗?还是我应该用希腊语讲啊?把阿波罗尼斯当定语,把圆当主语。。。就是一个圆,怎么被外国人名吓唬住了。”
结果,一分钟不到,题做出来了。学生还感叹着“这题也不难呢”。
虽然是个小插曲,但是我脑海里却跳出很多名词“蒙日圆”、“阿基米德三角形”、“塞瓦定理”、“海伦公式”等等,都是可以出现在高考题中的,比如2008年江苏卷13题就考了“阿波罗尼斯圆”。

其实我们成年人在面对陌生事物的时候无非也就两种态度。
①因为不懂,所以对它会不削一顾。
②因为不懂,所以觉得它特别牛哔!
本来不难的问题,因为名词陌生,所以感觉困惑,会有畏惧心理,可能造成丢不该丢的分,可能会因为一分之差。。。想想都可怕!
言归正传,今天聊聊“阿波罗尼斯圆”
公元前3世纪,古希腊数学家阿波罗尼斯在前人的基础上写了一部划时代的著作《圆锥曲线论》,该书给出了当时数学家们所研究的六大轨迹问题,其中之一便是“到两个定点的距离之比等于不为1的常数的轨迹是圆”,简称“阿氏圆”。
这里我用一个动图来说明下这个轨迹,一目了然。
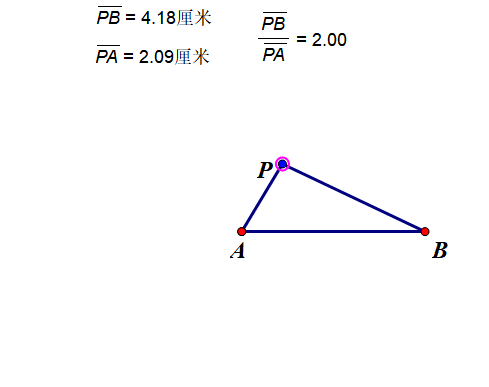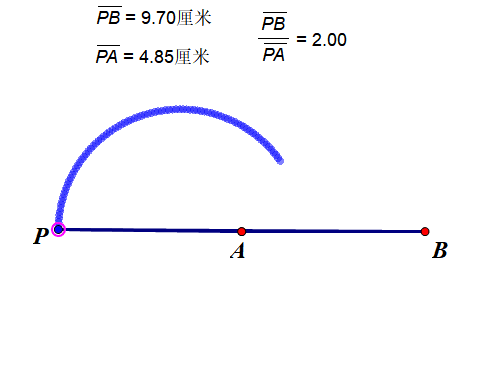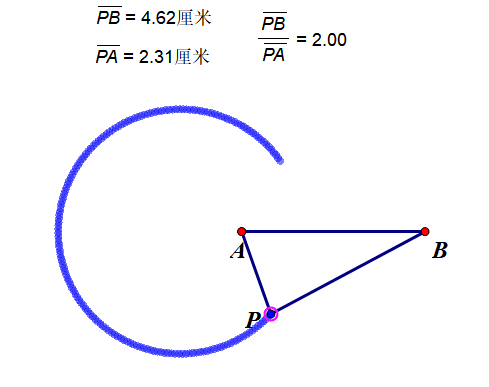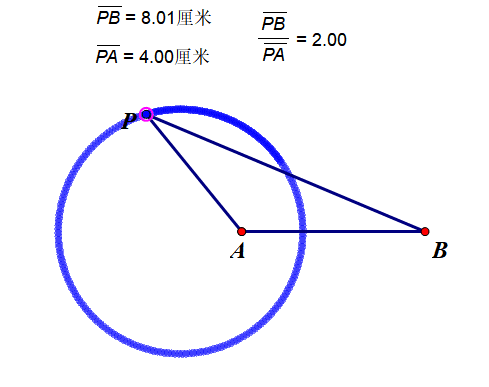
看,多圆!
轨迹知道了,怎么计算轨迹方程呢
轨迹方程三步走,设点,找等,化简。
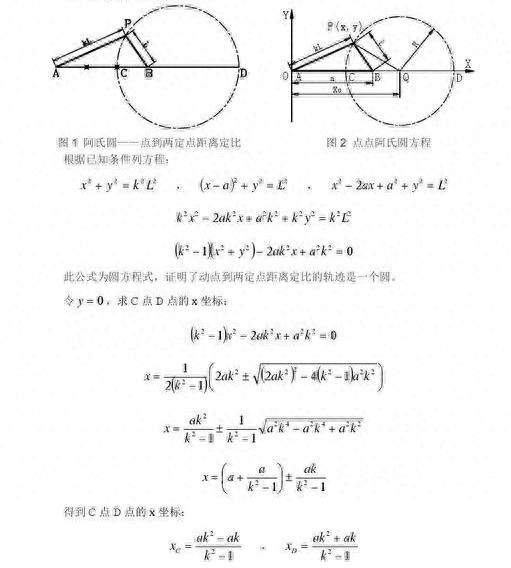
求出C和D的横坐标,圆心Q是CD中点。

这里a是AB线段长度,k是到两定点的距离比。知道了圆心和半径,就变成我们最熟悉的圆了。
阿波罗尼斯圆有哪些性质






阿波罗尼斯圆在生活中的应用
在建筑设计中,比如拱桥桥洞。

比如自行车轮距。

你还能想到哪些,欢迎一起讨论。
结束语
其实高考题没那么难,至少比平时的模拟考题简单。高考数学以“新”题为主,新在哪儿?都是题干新颖,题意新鲜,题型一般。
高考越来越喜欢结合生活,越来越喜欢回顾数学史。那我们就多关注关注。
以成年人的角度先观察自己对新鲜事物的理解,再去理解孩子们看到新鲜事物的感觉。那我们就先从心理上解决对陌生的恐惧。
不懂没事儿,可以学。
不会没事儿,可以学。
学会学习,强过做题。

毛老师原创文章。
标签: