傅里叶变换的意义和理解_傅里叶变换的意义作用

傅里叶变换的意义和理解。这些内容对于提高学生的物理思维能力，培养学生的创新精神和实践能力有重要意义。本书可作为高等院校物理专业的教材，也可供广大科技技工作者和高等院校师生参考。同时，本书还可作为大专院校物理教学的参考书，以及相关研究人员的参考书。《物理学基础(第2版)(修订版))》由中国科学院院士、著名物理学家周立伟主编，北京大学出版社出版。

一、傅里叶变换的意义？

傅里叶变换的作用就是把非正余弦 周期（请注意必须是周期函数）函数转化为无限个规则的正弦余弦函数。

          变成规则的函数以后，虽然有无限项，但是工程取前几项精度就够用了。规则函数利于计算。

         把难以计算甚至无法计算的函数转化为可以计算的函数。 

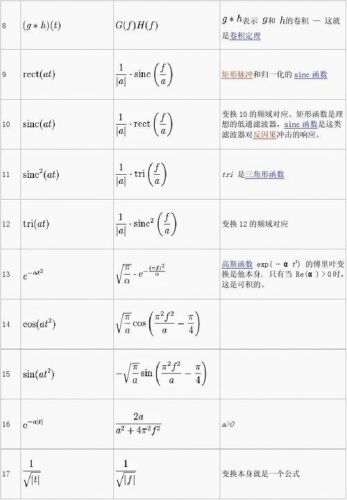
举例：最前面近似矩形的函数，就是有后边彩色各个无限项组成的。就是用傅里叶函数分解成后边无穷多个规则正余弦函数的。

二、傅里叶变换、拉氏变换的物理意义是什么？

傅式变换的目的是求解时域信号的频域组成成分。拉式变换其目的是为了快速求解常系数微分方程。

离散傅立叶变换为傅立叶变换的特殊形式，就是要分析的时域信号是离散的。

z变换就是对离散系统的数学模型——差分方程转化为简单的代数方程，使求解简单化。 前两个针对连续的，后两个针对离散的。傅式是时频域变换，拉式是求解方程。

三、傅里叶变换不同维度的物理意义？

优质答案1：

傅里叶变换在不同维度中具有不同的物理意义。以下是傅里叶变换在一维、二维和三维空间中的物理意义：

1. 一维傅里叶变换：

   - 时域（时间域）信号转换到频域：在时域中，傅里叶变换将一个函数从时间域转换到频域。它将一个信号表示为不同频率的正弦和余弦波的叠加。通过傅里叶变换，我们可以分析信号的频谱特性，如频率成分、频率强度等。

   - 空域（空间域）信号的周期性分析：在空域中，一维傅里叶变换可以应用于周期性信号的分析。它可以将周期性信号表示为一系列频率分量的叠加，从而得到信号的频谱信息。

2. 二维傅里叶变换：

   - 图像处理与频域滤波：在二维图像处理中，傅里叶变换用于将图像从空域转换到频域。这使我们能够分析图像的频谱特征，并应用频域滤波来实现图像增强、去噪、边缘检测等操作。

   - 信号的时频分析：二维傅里叶变换也可以用于时频分析，例如在语音信号处理和音频处理中，它可用于分析信号的频谱特性随时间的变化。

3. 三维傅里叶变换：

   - 空间频率分析：在三维空间中，傅里叶变换可以应用于空间频率分析。例如，在三维图像处理和计算机视觉中，可以使用三维傅里叶变换来分析物体的形状、纹理和结构。

   - 体积数据处理：三维傅里叶变换在医学成像领域中被广泛应用，用于处理体积数据（如CT扫描、MRI等）。它可以用于图像重建、空间滤波、特征提取等应用。

总之，傅里叶变换在不同维度的物理意义包括频域分析、时频分析、空间频率分析以及信号和图像的变换和处理。它在多个领域中都具有重要的应用，包括信号处理、图像处理、声音处理、通信等。

优质答案2：

从纯粹的数学意义上看，傅里叶变换是将一个函数转换为一系列周期函数来处理的。

从物理效果看，傅里叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅里叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，傅里叶逆变换是将图像的频率分布函数变换为灰度分布函数。

在二维情况下，傅里叶变换转换的是一个图像矩阵中的每个像素点，将每个像素点的坐标映射到一个复平面中，即复数坐标系。在这个复数坐标系中，每个像素点的坐标是一个复数，表示该像素点具有的频率信息。因此，傅里叶变换在二维情况下的物理意义是将一个二维图像中的每个像素点的灰度值变换为该像素点在水平和垂直方向上的频率信息。

简而言之，傅里叶变换不同维度的物理意义在数学上是一致的，而在实际应用中，不同维度下的物理意义会有所不同，需要根据具体问题背景进行理解。