奇函数减偶函数是什么函数（如何判断函数奇偶性口诀）

运用函数的奇偶性与单调性的关系是进行区间转换的一种有效手段。奇函数在对称区间上的单调性相同，且

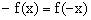
。偶函数在对称区间上的单调性相反，且

。

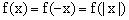
例1、求解方程

。

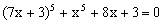
解：设函数

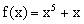
，则是奇函数而且单调递增。原方程等价于

，于是有

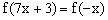
，即

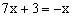
，得

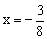
为所求方程的解。

例2、若定义在（－1，1）上的奇函数是减函数，且有

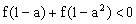
，求实数a的取值范围。

解：由

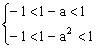
，解得

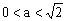
，再由，得

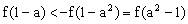
。因f(x)为奇函数且为减函数，所以，可得

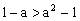
，解不等式

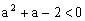
，得

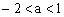
。综上可得

。

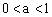
例3、设是定义在［－1，1］上的奇函数，且对任意实数a、b∈［－1，1］，当

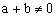
时，都有

。

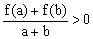
（1）若a>b，试比较

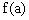
与

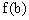
的大小。

（2）解不等式

。

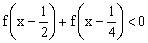
解：（1）由a>b，得

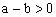
，即

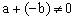
，由题意可得

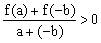
。因是奇函数，所以

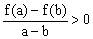
，可得

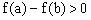
，即

。

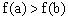
（2）由（1），显然是定义在［－1，1］上的增函数，仿例2，易求出不等式的解为

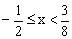
（同学们不妨自己动手试一试）。

–END–

运用函数的奇偶性与单调性的关系是进行区间转换的一种有效手段。奇函数在对称区间上的单调性相同，且

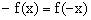
。偶函数在对称区间上的单调性相反，且

。

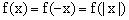
例

1、

求解方程

。

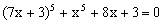
解：设函数

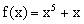
，则

是奇函数而且单调递增。原方程等价于

，于是有

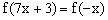
，即

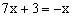
，得

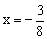
为所求方程的解。

例

2、

若定义在（－

1

，

1

）上的奇函数

是减函数，且有

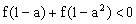
，求实数

a

的取值范围。

解：由

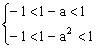
，解得

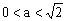
，再由

，得

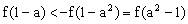
。因

f(x)

为奇函数且为减函数，所以

，可得

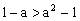
，解不等式

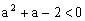
，得

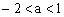
。综上可得

。

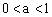
例

3、

设

是定义在［－

1

，

1

］上的奇函数，且对任意实数

a

、

b

∈［－

1

，

1

］，当

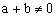
时，都有

。

（

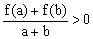
1

）若

a>b

，试比较

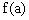
与

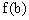
的大小。

（

2

）解不等式

。

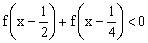
解：（

1

）由

a>b

，得

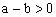
，即

，由题意可得

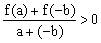
。因

是奇函数，所以

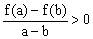
，可得

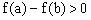
，即

。

（

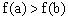
2

）由（

1

），显然

是定义在［－

1

，

1

］上的增函数，仿例

2

，易求出不等式的解为

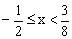
（同学们不妨自己动手试一试）。

–END–

长按图片点关注，学习路上不迷路！