真子集符号怎么读？真子集符号有几种写法

真子集符号怎么读？这个问题困扰了很多人，今天我们就来解决这个问题。首先我们要知道日语中的符号是怎么来的，其实符号就是汉字的一部分，我们平时说的的日语就是汉字的日语。那么日语中的汉字有哪些呢？下面我们一起来看看吧。首先我们要知道日语中的汉字有哪些？下面我们一起来看看吧。

一：真子集符号怎么读

真子集的符号写为⫋。

如果 *** A⊆B，存在元素x∈B，且元素x不属于 *** A，我们称 *** A与 *** B有真包含关系， *** A是 *** B的真子集（proper subset）。记作A⫋B（或B⫌A），读作“A真包含于B”（或“B真包含A”）。

真子集与子集的区别：

子集就是一个 *** 中的全部元素是另一个 *** 中的元素，有可能与另一个 *** 相等。

真子集就是一个 *** 中的元素全部是另一个 *** 中的元素，但不存在相等。

非空真子集：如果 *** A⫋B，且 *** A≠∅， *** A是 *** B的非空真子集（nonvoid proper subset）。

二：真子集符号怎么打进word

R是一门编程语言。

因为R语言是一种面向数据分析和统计建模的编程语言，它提供了丰富的数据分析函数和可视化工具，被广泛应用于科学研究、商业分析和数据挖掘等领域。

此外，R语言还具有开源、免费、跨平台等优点，受到了越来越多人的

三：真子集符号怎么写

零件之间的配合（尺寸关系）对产品性能有重要影响。

实际制造的零件，总是和几何学上的理想形状有偏差。这个偏差在图纸上表现为尺寸公差。这样，一个尺寸就有了最大值和最小值。

将产品中轴、孔概念稍稍扩大一下：圆柱形和非圆柱形内表面（如键槽），统称孔；相应地，外表面（如键）就统称为轴。ASME Y14.5中的Feature of Size（尺寸形体，也有叫尺寸特征、尺寸元素的）也是这个含义。

物理知识告诉我们，物质都是原子组成的。所谓最大实体状态，其实就是零件包含最多原子时的状态；相应地，最小实体状态时原子最少。最大实体状态和尺寸值的关系如表1。

表1. 实体状态和尺寸值

如果直径最大时的轴都比直径最小时的孔还要小，那么轴更小孔更大时，显然可以保证轴轻松过孔。引入"最大实体状态"的概念，只是为了方便讨论间隙装配问题。

一、扫掠形成空间实体

马克思有句名言：一门科学只有在成功地运用数学时，才算达到了真正完善的地步。在ASME的GD&T（Geometric Dimensioning and Tolerancing，几何尺寸与公差）标准体系中，ASME Y14.5.1M就是在GD&T中运用了数学。

在三维空间（立体空间）中，让直径为d的实心球的球心沿着空间三维曲线扫掠，可以得到实心管（特殊的三维实体）。同样，如果沿着空间三维曲面扫掠，则可以得到三维实体。参见图1。

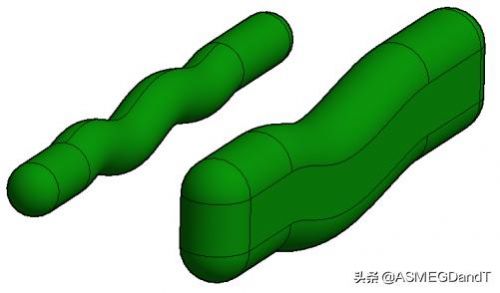
图1. 扫掠形成三维实体

二、轴（外特征）的极限尺寸

假设轴的尺寸为20±0.2。用直径为20+0.2（最大实体状态下的尺寸dMMC）的实心球沿某条空间曲线Sm扫掠得到实心管Gm。用直径为20-0.2（最小实体状态下的尺寸dLMC）的实心球沿沿某条空间曲线Sl扫掠得到实心管Gl。对于实际制造出来的轴，如果满足如下条件，则符合尺寸要求：

1) 上述空间曲线Sm和Sl都存在，且使得

2) Gm能将Gl完全包含在内（即Gl⊂Gm，⊂是 *** 运算的真子集符号）

3) 轴的外表面F能被Gm-Gl（-是 *** 的差运算符号）完全包含在内（F⊂Gm-Gl）

4) 轴的外表面F能将Gl包围

通俗直观的理解：最大实体尺寸和最小实体尺寸这两个极限尺寸，通过简单的数学加减运算得到；实心球是几何意义上完美的球；空间曲线Sm和Sl是立体空间中的任意曲线，相互之间没有任何位置关系要求；轴的外表面F是空间曲面；Gl在F内，而Gm在F外，这样自然就满足要求Gl⊂Gm、F⊂Gm-Gl。

对于某个实际的轴外表面F，不大于dMMC且能满足上述条件1)、2)、3)、4) 的最小直径，就是该轴的实际尺寸（比如20.10、20.19、19.80等等）。

三、孔（内特征）的极限尺寸

假设孔的尺寸20±0.2，则其最大实体状态下的尺寸dMMC为20-0.2；最小实体状态下的尺寸dLMC为20+0.2。实际孔是否满足尺寸要求，参照轴进行类推。

四、非圆柱形轴、孔的极限尺寸

对于非圆柱形特征，只需把上述空间曲线替换成空间曲面（Sm和Sl）。其余类推。

五、包容原则

在ASME Y14.5中，默认适用包容原则（规则#1），也常说成"尺寸公差也控制形状"。在数学意义上的理解，就是对前述Sm增加"理想形状"这一要求。即如果Sm是空间曲线，则此时必须是直线（适用于圆柱形轴和孔）；如果Sm是空间曲面，则此时必须是平面（适用于非圆柱形轴和孔，如键和键槽）。对于Sl，则没有特别要求，仍然可以是任意空间曲线或曲面。

六、举例图解

最后，图2以轴为例，图解说明最大和最小尺寸在独立原则和包容原则下的含义。

图2. 最大和最小尺寸在独立原则和包容原则下的含义